递归算法入门

Twisuki2025/10/4约 3652 字大约 12 分钟

递归算法入门

又咕咕好长时间了, 这次有朋友初学py, 被递归难住(尤其是汉诺塔问题), 因此写了一篇博客, 简单讲解下递归算法的算法核心.

在讲解之前, 要先说明一个最大的误区: 算法是解决问题的方法, 思路, 流程, 不过是体现在代码里, 当然你可以以任何方式体现它, 包括数学.

但注意的是, 算法不是数学的概念, 数学需要算法, 而非算法拘泥于数学.

因此, 很多人理解递归出现问题, 大部分就在这里. 使用数学语言解释是简洁明了的, 但这不代表它和数学有关系, 更不代表它依赖于数学.

1. 数学上的递归算法

1.1 阶乘

递归最经典的问题便是阶乘, 但我认为阶乘并不适合递归, 一般人看到阶乘的想法实际上是:

n! = n \times (n - 1) \times (n - 2) \times ... \times 1

已经被很简单的拆开了, 没有人会愿意找 $n$ 和 $n - 1$ 的关系:

n! = {n \times (n - 1)!, 1, n > 1 n = 0, 1

所以它并不是一个好例子, 我们直接看斐波那契数列

1.2 斐波那契数列

斐波那契数列是最经典的例子之一, 它的定义是后一项等于前两项之和, 即:

f ib (n) = f ib (n - 1) + f ib (n - 2)

我们补充下初始条件, 则为:

f ib (n) = {f ib (n - 1) + f ib (n - 2), 1, n > 2 n = 1, 2

转换成代码语言:

python

def fib(n):
    if n <= 2:
        return 1
    return fib(n - 1) + fib(n - 2)

javascript

function fib(n) {
	if (n <= 2) return 1
    return fib(n - 1) + fib(n - 2)
}

int fib(int n) {
    if (n <= 2) return 1;
    return fib(n - 1) + fib(n - 2);
}

以上都是老生常谈的内容, 对你的理解没有多余的帮助, 我们开始思考递归的本质.

因为 $n$ 能被拆到 $n - 1$ 和 $n - 2$ , 那么 $n - 1$ 就能拆到 $n - 2$ 和 $n - 3$ , 接下来的 $n - 4, n - 5, \dots$

停!

如果你在数学的角度考虑, 那最后会到 $1$ , 这是毋庸置疑的. 但是从算法到角度考虑, 我们知道 $n$ 会减小, 这就意味着问题的规模在减小, 此外我们还知道有限规模的问题可以解决, 这才是递归的两个条件:

可以分解成更小规模的问题, 且有限规模的问题可以解决.

我们现在要抛弃数学语言了, n都不想要.

1.3 青蛙跳台阶

共 $n$ 级台阶, 青蛙每次可以跳 $1$ 级或 $2$ 级, 问有多少种跳法?

抛弃数学语言吧, 我们开始分析这个问题为一个函数:

如果青蛙先跳 $1$ 级, 那么接下来需要 $n - 1$ 级需要"青蛙跳".
如果青蛙先跳 $2$ 级, 那么接下来需要 $n - 2$ 级需要"青蛙跳".

这就是问题规模的缩小.

如果只有一级台阶, 那么只有一种跳法.
如果有两级台阶, 那么有 $(1, 1)$ 和 $(2)$ 两种跳法.

这就是有限规模的问题可以解决.

因此, 我们可以写出:

换成程序的语言:

Q: 先跳 2 级台阶, 为什么还是 1 * frog(n - 2), 跳两级不是有 (1, 1), 和 (2) 两种跳法吗?
A: 先跳两级的 (1, 1) 跳法在先跳一级中已经被包括了, 不需要重复计算.

写出来发现和斐波那契数一样的.

2. 快速排序

上面几个例子都是数学问题, 只是算法在数学上的应用, 尽管第三个问题有个实际的背景, 不是纯粹的数学问题, 但是仍然是个给你一个数, 求出一个数的数学问题, 我们还没用算法来真正"做事".

很多人前两个听懂了理解了, 但是到了汉诺塔就懵了, 其实是因为汉诺塔不是数学问题, 不要你算东西, 而是要你去"做事", 但学习了12年数学的我们怎么会用数学做事呢.

所以在汉诺塔之前, 我插了个快速排序的例子, 来体会一下算法是如何做事的(毕竟汉诺塔太抽象了, 除了递归之外, 它做的事也挺复杂的).

我们直接看一下快速排序的代码实现(这里展示的是"非原地排序"版本, 比较简单, 但C语言不太好写):

python

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x <= pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)

javascript

function quickSort(arr) {
    if (arr.length <= 1) return arr;
    const pivot = arr[arr.length / 2];
    const left = arr.filter(x => x <= pivot);
    const middle = arr.filter(x => x === pivot);
    const right = arr.filter(x => x > pivot);
    return [...quickSort(left), ...middle, ...quickSort(right)];
}

我们用伪代码说说它到底"干了个什么事":

对数组 arr 快速排序 {
    如果 arr 长度为 1 或 0: 直接返回 arr
    
    令 pivot = 数组最中间的数
    数组 left = arr 中所有小于 pivot 的数
    数组 middle = arr 中所有等于 pivot 的数
    数组 right = arr 中所有大于 pivot 的数
    
    返回 对数组 left 快速排序 + 数组 middle + 对数组 right 快速排序
}

它是怎么缩小问题规模的:

取最中间的数
比它小的放左边, 比它大的放右边, 和它相等的放中间, 这样无论左右如何, 中间的数位置都正确了.

25647378 left \underline{6381015} \underline{19} 810331519 middle \underline{1919} right \underline{25477833}

现在左右两个数组等待排序, 虽然要排序的东西变多了, 但是它们两个必然比原来数组要小

这就是问题规模的缩小.

当数组长度为 $1$ 或 $0$ 时, 不需要排序.

\underline{6}

这就是有限规模的问题可以解决.

理解是怎么分解事件的了吗?

3. 汉诺塔问题

背景, 题干什么的不讲了. 我们把三个塔叫做 L, M, R(也有叫A, B, C的, 不过这里还是叫左, 中, 右吧).

已经知道它是个递归问题了, 那么就从两个条件入手.

有限规模的问题可以解决, 这是废话, 只有一块盘子可以随便移动.
问题规模的缩小, 那么怎么缩小呢?

问题规模的缩小意味着汉诺移动 n 块盘子可以分解成汉诺移动 n - 1 块盘子. 我们不需要去考虑汉诺移动 n - 1 块盘子怎么实现的, 我们只知道, 现在有办法一次性的移动 n - 1 块盘子了.

既然我们可以一次性的移动 n - 1 块盘子, 那么移动 $n$ 块盘子就很简单了:

开始.

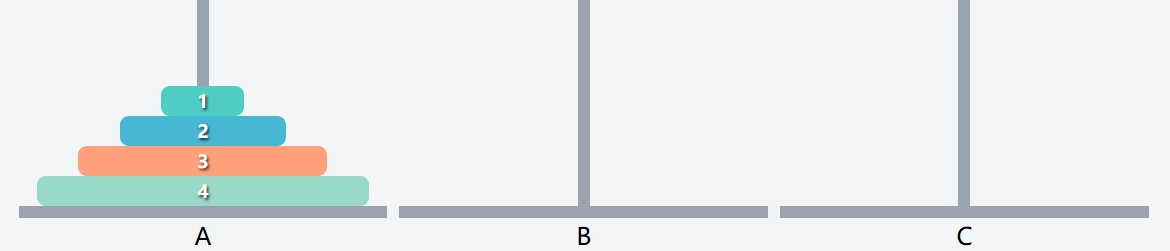
别管怎么移的, 因为在讨论递归, 所以我们先一次移动 n - 1 个盘子, 至于这 n - 1 个盘子的细节, 交个 n - 2 的递归去考虑, 现在不用管.

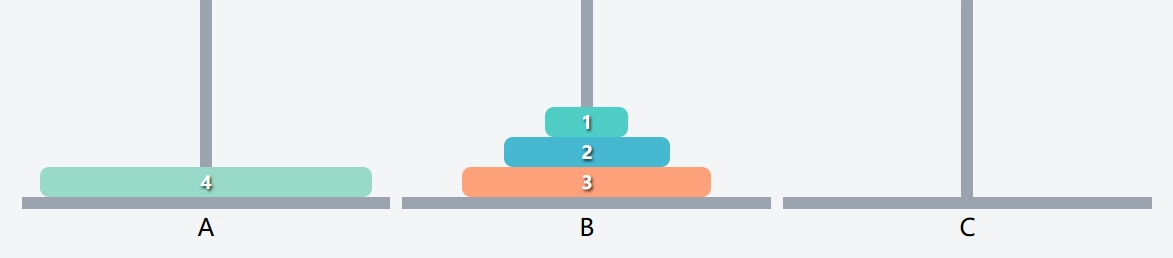
最下面一个盘子直接移过去.

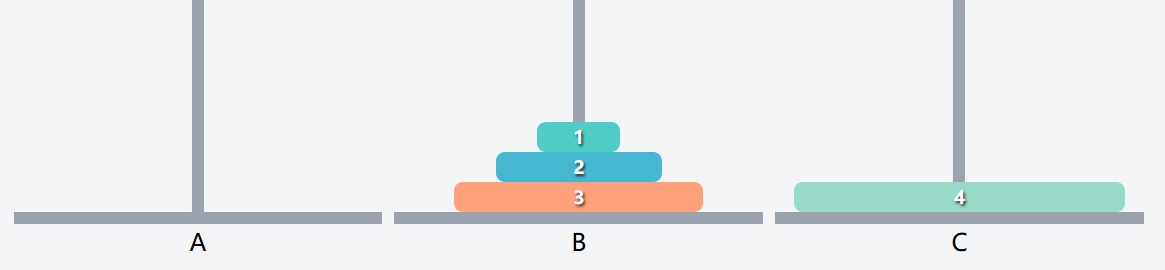
同样的, 别管怎么移的, 最后再一次移动 n - 1 个盘子, 完成问题.

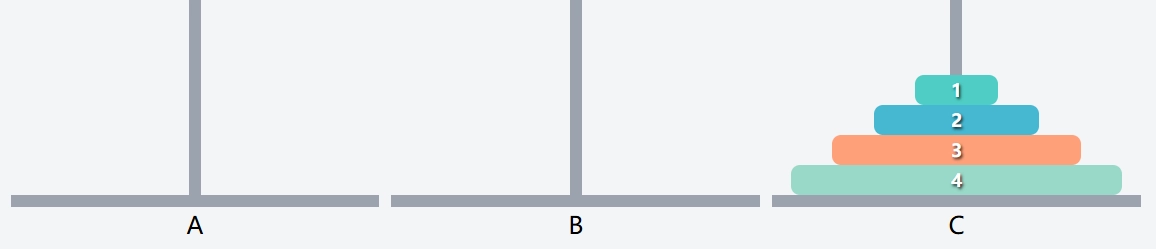
拆解成功! 现在第二个条件也满足了, 移动 n 个盘子的问题变成移动 n - 1 个盘子的问题了, 虽然它被执行了两次, 但规模还是缩小了.

递归的部分已经结束了, 接下来我们要用代码把它展示出来, 这是另一大难点.

请确保递归部分已经没问题了.

代码展示也很难, 导致很多人汉诺塔问题理解不能, 请补药归咎于递归!

对于汉诺塔函数, 我们先明确它在干什么.

Q: 为什么要输入 $3$ 个塔呢, 怎么输入?
A: 汉诺塔函数可以描述为: "汉诺塔移动法, 移动 n 层, 从塔1经塔2到塔3", 没有塔2的辅助是移动不过去的.
所以我们把这三个塔分别命名为起始塔, 辅助塔, 目标塔, 即 start, helper(也有写作via的), target.
最开始的问题可描述为: 从左塔经中间塔移动到右塔, 即 start = "L", helper = "M", target = "R".

则函数声明如下:

python

def hanoi(n, start, helper, target):
    ...

hanoi(4, "L", "M", "R")

javascript

function hanoi(n, start, helper, target) {
    
}

hanoi(4, "L", "M", "R");

void hanoi(int n, char start, char helper, char target) {
    
}

int main() {
    hanoi(4, "L", "M", "R");
}

接下来实现具体的逻辑, 先看伪代码:

汉诺塔移动 n 层, 从 start 经 helper 到 target {
    如果 n 为 1: 直接把盘子从 start 移动到 target, 结束
    
    汉诺塔移动 n - 1 层, 从 start 经 target 先放到 helper
    把最下面剩下的盘子从 start 移动到 target
    汉诺塔移动 n - 1 层, 再把 helper 的塔 start 移到 target
}

注意这里start, helper, target三个变量的传递, 这里是写成函数最容易懵的地方.

Q: 为什么不写L, M, R了?
A: 因为参与运算的根本就不是L, M, R.
最初是 L 经 M 到 R, 但其中移动 n - 1 层时, 是 L 经 R 到 M, 从起始塔到辅助塔, 三个塔的职能变了.
也就是说, 函数的运行中, L, M, R三个塔到底谁到谁, 一直都在变, 不变的只有起始塔, 辅助塔, 目标塔这三个角色的关系.
因此我们传递变量, 不传递值.
变量是抽象的, 难以理解很正常, 好好想想他们的关系吧. 心里默念从起始移到目标, 不是从左移到右.

代码如下, 理解了再来抄:

python

def hanoi(n, start, helper, target):
    if n == 1:
        print(f"{start} => {target}")
        return
    hanoi(n - 1, start, target, helper)
    print(f"{start} => {target}")
    hanoi(n - 1, helper, start, target)

hanoi(4, "L", "M", "R")

javascript

function hanoi(n, start, helper, target) {
    if (n === 1) {
        console.log(`${start} => ${target}`);
        return;
    }
    hanoi(n - 1, start, target, helper);
    console.log(`${start} => ${target}`);
    hanoi(n - 1, helper, start, target);
}

hanoi(4, "L", "M", "R");

void hanoi(int n, char start, char helper, char target) {
    if (n == 1) {
        printf("%c => %c\n", start, target);
        return;
    }
    hanoi(n - 1, start, target, helper);
    printf("%c => %c\n", start, target);
    hanoi(n - 1, helper, start, target);
}

int main() {
    hanoi(4, "L", "M", "R");
}

4. 扫雷的扩散算法

写一下汉诺塔算法, 写不下来还是没理解, 别往下看.

算法是用来解决问题的, 但是汉诺塔你知道可以用递归来解决, 于是用递归的方式分析, 做出来了.

实际情况是问题为主导, 你不清楚要干什么. 但是用不用递归, 特征很明显.

上面归纳的两条只是递归解决问题时候要考虑到地方, 我们直接举个实际例子.

扫雷中, 当你点开一个空格子(没有数字, 意味着周围都没有雷), 那么它会发生"扩散", 也就是把周围的格子都打开, 如果周围的格子也是空格子, 那么继续扩散.

它有着很明显的递归特征, 尽管你很难用缩小问题规模和有限规模的问题可以解决来描述它.

它的特征在哪呢? 当翻开格子为空格子时, 这时发生"扩散", 程序的语言讲叫做执行spread()函数, 扩散到空格子时, 还会扩散, 意味着spread()函数中一定调用了spread()函数, 自己调用了自己, 这就是递归.

有限规模的问题可以解决, 只有空格子能扩散, 都是数字就不扩撒了, 同时注意已被翻开的格子也不能扩散.

A B A B A B ■ B 当对 A 执行 spread() 函数时, 它会对 B 执行 spread() 函数 这是如果不对 A 做任何标记, B 又会对 A 执行 spread() 函数 A 再次对 B 执行 spread() 函数, 造成死循环, 这是错误做法 A 执行后立即 " 翻开 ", B 就不会再对 A 执行 spread() 函数, 正常扩散下去 (或终止)

问题规模的缩小, 我们根本不知道问题规模有多大(要扩散多少格子), 但是每次扩散一个格子, 问题规模必然变小了 $1$ , 这就够了, 因为问题规模是有限的.

这里展示一部分代码:

python

def spread(x, y):
    if map[x][y].is_turned():  # 已翻开, 结束
        return
    map[x][y].turn()  # 翻开格子
    if map[x][y].is_number():  # 数字不扩散
        return

    # 这是在二维格子中安全遍历一个格子周围的方法, 这里可以先不去理解
    for dx in [-1, 0, 1]:
        for dy in [-1, 0, 1]:
            if 0 <= x + dx < width and 0 <= y + dy < height:
                if dx == 0 and dy == 0:
                    continue  # 自己不参与运算

                i, j = x + dx, y + dy
                if map[i][j].is_blank():
                    spread(i, j)  # 空格子, 递归扩散
                if map[i][j].is_number():
                    map[i][j].turn()  # 数字, 直接翻开

javascript

function spread(x, y) {
	if (map[x][y].isTurned()) return; // 已翻开, 结束
    map[x][y].turn(); // 翻开格子
    if (map[x][y].isNumber()) return; // 数字不扩散
    
    // 这是在二维格子中安全遍历一个格子周围的方法, 这里可以先不去理解
    for (const dx of [-1, 0, 1]) {
	    for (const dy of [-1, 0, 1]) {
            if (x + dx >= 0 && x + dx < width && y + dy >= 0 && y + dy < height) {
				if (dx === 0 && dy === 0) continue; // 自己不参与运算
                
                const i = x + dx, j = y + dy;
                if (map[i][j].isBlank()) spread(i, j); // 空格子, 递归扩散
                if (map[i][j].isNumber()) map[i][j].turn(); // 数字, 直接翻开
            }
		}
    }
}

~~至于为什么不展示C语言代码, 你看我写的能跑吗~~