线性回归 - 波士顿房价预测

Twisuki2025/4/13约 3872 字大约 13 分钟

上个世纪70年代, 波士顿地区房价波动较大, 这对房地产市场参与者是个重大的挑战. 为了解决这个问题, 研究人员使用机器学习算法来预测房价.

本人是人工智能专业学生, 第一次接触到机器学习便是这个算法(例题). 花费了大概两天时间, 完成了老师布置的波士顿房价预测的问题.

但是, 使用诸如numpy, panda, paddle等库完全不能理解线性回归, 梯度下降的逻辑和思想.

因此, 我使用纯py原生库编写了波士顿房价预测的机器学习代码(但是使用了plt库用于绘图), 下面分享一下.

data.txt数据来源于飞桨平台

1. 线性回归与梯度下降

当我们进行数据分析时, 需要想办法找到一个函数 $y = f (x_{1}, x_{2}, \dots, x_{n})$ 拟合这样一组数据, 那么如何找到这样一个函数 $f$ 呢.

1.1 线性回归算法

有些数据因变量和各个自变量都成线性关系, 即对于自变量 $x_{i}$ , 可以有 $Δ y \propto Δ x_{i}$ , 即每个自变量都以一次函数的形式影响因变量, 而非二次函数或对数指数等其他形式, 这样的关系成为 线性关系.

那么对于 $n$ 个自变量的数据, 可以构建这样的拟合函数:

y = k_{1} x_{1} + k_{2} x_{2} + \dots + k_{n} x_{n} + b

里面共有 $k_{1}, k_{2}, \dots, k_{n}, b$ $n + 1$ 个参数, 我们所需的就是将这 $n + 1$ 个参数找出来.

显然, 数据量较大时, 我们任取几组数据, 构建方程组:

⎩ ⎨ ⎧ y_{1} = k_{1} x_{11} + k_{2} x_{12} + \dots + k_{n} x_{1 n} + b y_{2} = k_{1} x_{21} + k_{2} x_{12} + \dots + k_{n} x_{1 n} + b \dots\dots\dots\dots y_{n} = k_{1} x_{n 1} + k_{2} x_{n 2} + \dots + k_{n} x_{nn} + b y_{n + 1} = k_{1} x_{n + 1, 1} + k_{2} x_{n + 1, 2} + \dots + k_{n} x_{n + 1, n} + b

通过矩阵运算解出 $k_{1}, k_{2}, \dots, k_{n}, b$ $n + 1$ 个参数, 就能得到一个函数.

矩阵运算求解这样的方程组对于计算机来说并不麻烦. 然而, 当我们用 $n + 1$ 组数据得到方程时, 当我们代入第 $n + 2$ 个数据时, 很可能不符合甚至很大误差.

所以, 我们要使用一定的方法来求解这组参数.

对于这组数据, 构建线性回归方程:

\overset{y}{^} = λ_{1} x_{i} + λ_{2} x_{2} + \dots + λ_{n} x_{n} + δ

其中 $\overset{y}{^}$ 为预测值, $λ_{1}, λ_{2}, \dots, λ_{n}$ 为回归系数或权重参数, $δ$ 为 截距参数.

1.2 残差平方和

在研究如何优化参数之前, 我们先研究如何衡量参数质量.

定义残差为 $r = y - \overset{y}{^}$ , 即y真 - y估. 残差越小, 拟合就越标准, 参数质量越高.

当然我们不能只拘泥于一组数据, 我们计算所有组的残差 $r_{i} = y_{i} - \overset{y}{^}_{i}$ . 定义残差平方和:

RSS = i = 1 \sum n r_{i}^{2} = i = 1 \sum n (y_{i} - \overset{y}{^}_{i})^{2}

RSS(残差平方和)一定是正数的和, 保证了不会存在一正一负相互抵消的结果. 此外, 平方和也使得后续求导操作更加简洁.

残差平方和反映了拟合的质量, 所以我们要选取更好的参数, 使该值变得更小.

1.3 线性回归参数的优化

上面已经指明了参数优化的方向, 那么, 参数如何调整能使RSS变低呢?

这时我们将参数作为自变量, RSS作为因变量, 它们之间构成的函数是明显的:

RSS = i = 1 \sum n (y_{i} - \overset{y}{^}_{i})^{2} = i = 1 \sum n (y_{i} - (λ_{1} x_{i 1} + λ_{2} x_{i 2} + \dots + λ_{n} x_{in} + δ)^{2}

对于二元函数 $y = f (x)$ , 在某点 $x = x_{0}$ 求出 $k = f^{'} (x_{0})$ . 如果 $k > 0$ , 则 $x$ 减小, $y$ 减小; 反之 $k < 0$ , 则 $x$ 增大, $y$ 减小.

即, 欲使 $y$ 减小, $x$ 需朝着 $- k$ 的方向移动, 这样能找到局部的最优解.

虽然局部最优不一定为全局最优, 但是, 该方法保证我们起码可以找到附近的一个最优解

同理, 对于多元函数 $y = f (x_{1}, x_{2}, \dots, x_{n})$ , 求出 $y$ 对各个自变量的偏导数 $\frac{\partial f}{\partial x _{i}}$ , 构成向量:

\nabla f = (\frac{\partial f}{\partial x _{1}}, \frac{\partial f}{\partial x _{2}}, \dots, \frac{\partial f}{\partial x _{n}})

该向量称为 $f$ 的方向导数, 又称梯度.

我们计算某初始点 $(x_{10}, x_{20}, \dots, x_{n 0})$ 的梯度 $\nabla f_{0}$ , 让各个自变量朝着 $- (\nabla f_{0})_{i}$ 的方向移动(或表述为沿着 $[\nabla f_{0}]_{i}$ 相反方向移动, 即梯度下降), 这样因变量 $y$ 就能变小.

那么对于参数的优化也是如此, 只不过要把 $n + 1$ 个参数看做自变量, 去计算这些参数的梯度, 然后让这些参数进行梯度下降.

对于权重参数 $λ_{i}$ , 计算偏导数为:

\frac{\partial RSS}{\partial λ _{j}} = \frac{\partial}{\partial λ _{j}} (i = 1 \sum n (y_{i} - \overset{y}{^}_{i})^{2}) = 2 i = 1 \sum n (y_{i} - \overset{y}{^}_{i}) \cdot \frac{\partial}{\partial λ _{j}} (y_{i} - \overset{y}{^}_{i}) = - 2 i = 1 \sum n (y_{i} - \overset{y}{^}_{i}) \cdot \frac{\partial y ^ _{i}}{\partial λ _{j}} = - 2 i = 1 \sum n (y_{i} - \overset{y}{^}_{i}) \cdot x_{ij} = - 2 i = 1 \sum n r_{i} \cdot x_{ij}

对于截距参数 $δ$ , 计算偏导数为:

\frac{\partial RSS}{\partial δ} = \frac{\partial}{\partial δ} (i = 1 \sum n (y_{i} - \overset{y}{^}_{i})^{2}) = 2 i = 1 \sum n (y_{i} - \overset{y}{^}_{i}) \cdot \frac{\partial}{\partial δ} (y_{i} - \overset{y}{^}_{i}) = - 2 i = 1 \sum n (y_{i} - \overset{y}{^}_{i}) \cdot \frac{\partial y ^ _{i}}{\partial δ} = - 2 i = 1 \sum n (y_{i} - \overset{y}{^}_{i}) = - 2 i = 1 \sum n r_{i}

综上, 得到梯度为:

\nabla RSS = (- 2 i = 1 \sum n r_{i} \cdot x_{i 1}, - 2 i = 1 \sum n r_{i} \cdot x_{i 2}, \dots, - 2 i = 1 \sum n r_{i} \cdot x_{in}, - 2 i = 1 \sum n r_{i})

接下来只要定义一组初始参数, 以及每次参数沿着梯度方向下降的步长(学习率), 让参数自动优化.

我们再定义一个精度(容差), 当梯度下降到这个位置时便跳出循环. 同时也要定义最大迭代次数, 防止无限计算.

2. 波士顿房价预测

import random
from typing import List
import matplotlib.pyplot as plt

2.1 数据处理

a) 数据导入

直接使用py原生库的open()函数导入数据, 将空格和换行分割的txt数据转化为二维数组.

同时float(_)将字符串转换为数字.

data = []
# 按行读取数据
with open("data.txt", 'r') as f:
    for l in f:
        # 按空格划分数据
        line = [float(_) for _ in l.split()]
        data.append(line)

print(f"data: {len(data)}, {len(data[0])}")
size = len(data)

b) 划分集

使用数据的0.8作为训练集, 用于训练模型; 剩下的0.2作为测试集, 用于最终测试.

划分之前, 需要先将数组随机打乱, 避免每次训练集都重复.

# 打乱数组, 确保集划分随机
random.shuffle(data)

# 计算大小
train_size = int(size * 0.8)

# 使用切片划分
train = data[:train_size]
test = data[train_size:]

print(f"train: {len(train)}, test: {len(test)}")

c) 数据标准化

由于数据有大有小, 有离散有连续. 为了防止每个参数移动步数过大, 我们需要对数据进行初始化处理.

初始化处理就是将各个指标同比例放大/缩小, 使其最终都落在[0, 1]区间内.

处理方法为:

x^{'} = \frac{x - x _{min}}{x _{ma x} - x _{min}}

或

x^{'} = \frac{x}{x ˉ}

# 计算均值
mean = [sum(_)/14 for _ in zip(*train)]

# 更新train和test
for row in range(len(train)):
    train[row] = [train[row][_] / mean[_] for _ in range(14)]

for row in range(len(test)):
    test[row] = [test[row][_] / mean[_] for _ in range(14)]

2.2 参数与函数

根据函数 $\overset{y}{^} = λ_{1} x_{i} + λ_{2} x_{2} + \dots + λ_{n} x_{n} + δ$ , 我们初始化参数并定义y和rss函数.

a) 定义参数

# 初始化参数
# lambda_1, lambda_2, ..., lambda_13, delta
para = [1 for _ in range(14)]

# 设置特征值(前13个变量)和目标值(最后一个变量)
features = [sample[:-1] for sample in train]
targets = [sample[-1] for sample in train]

b) 定义线性回归函数与残差函数

# 设置线性回归函数
def y(x: List[float], para: List[float]) -> float:
    return sum([para[_] * x[_] for _ in range(13)]) + para[13]

# 设置残差平方和函数
def rss(y_pred: List[float], y_true: List[float]):
    return sum([(y_pred[_] - y_true[_])**2 for _ in range(len(y_pred))])

2.3 机器学习

学习之前, 我们先测试一下上面的函数.

# 测试函数(在当前[1, 1, ..., 1]参数下计算残差平方和)
y_pred = [y(feature, para) for feature in features]
print(rss(y_pred, targets))

输出的RSS在822左右, 非常大.

a) 计算梯度

根据上面的数学推导, 我们直接编写:

def get_gradient(features, targets, para):
    # 计算残差
    r = [y(feature, para) - target for feature, target in zip(features, targets)]
    # 初始化梯度
    gradient = [0 for _ in range(14)]

    # 计算lambda偏导
    for i in range(13):
        gradient[i] = sum([r[_] * features[_][i] for _ in range(len(targets))])
    
    # 计算delta偏导
    gradient[13] = sum(r)

    return gradient

b) 梯度下降

梯度下降便是在梯度的基础上, 直接para -= gradient * learning_rate.

其中learning_rate为学习率, 代表每次更新参数的长度.

同时, 还有tolerance容差, 代表最终精度; max_itr迭代次数上限.

这些需要预先人为设置的参数称为超参数.

# 梯度下降函数
def gradient_descent(features, targets, para, learning_rate, tolerance, max_itr):
    # 迭代
    for itr in range(max_itr):
        # 计算梯度
        gradient = get_gradient(features, targets, para)
        
        # 检测是否达到精度
        if all(abs(_) < tolerance for _ in gradient):
            print(f"Done! Itr: {itr}")
            return para
        
        # 参数梯度下降
        para = [para[_] - learning_rate * gradient[_] for _ in range(len(para))]

    print(f"Can't keep up!")

    # 获取最优情况
    return para

c) 梯度下降函数的优化

上述函数有个明显的问题, 如果容差过小或学习率质量差, 迭代上限过小, 那么很容易Can't keep up!, 返回最后一次的para.

所以我们还要存储一个best_para并实时更新, 同时增加一个打印进度的输出.

# 梯度下降函数
def gradient_descent(features, targets, para, learning_rate, tolerance, max_itr):
    # 存储每次的运行结果(内存再见~)
    best_result = [*[0 for _ in range(14)], float("inf")]
    
    # 迭代
    for itr in range(max_itr):
        # 计算梯度
        gradient = get_gradient(features, targets, para)
        
        # 检测是否达到精度
        if all(abs(_) < tolerance for _ in gradient):
            print(f"Done! Itr: {itr}")
            return para
        
        # 参数梯度下降
        para = [para[_] - learning_rate * gradient[_] for _ in range(len(para))]

        y_pred = [y(_, para) for _ in features]
        if rss(y_pred, targets) < best_result[-1]:
            best_result = [*para, rss(y_pred, targets)]
            
        # 打印进度
        if itr % (max_itr // 10000) == 0:
            print(f"Itr: {itr}, Progress: {itr / max_itr * 100:.2f}%, RSS: {best_result[-1]:.2f}", end="\r")

    print(f"Can't keep up!")

    # 获取最优情况
    return best_result[:-1]

2.4 应用

a) 函数应用

接下来就可以进行应用了.

一组不会Can't keep up!的超参数:

learning_rate = 0.0001
tolerance = 1
max_itr = 5000

代码如下:

# 设置超参数
learning_rate = 0.0001
tolerance = 1
max_itr = 5000

# 开始运行
optimized_para = gradient_descent(features, targets, para, learning_rate, tolerance, max_itr)
print(f"Optimized Para: {optimized_para}")
y_pred_optimized = [y(_, optimized_para) for _ in features]
print("Optimized RSS:", rss(y_pred_optimized, targets))

同时我又测试了learning_rate = 0.000001, tolerance = 0.01, max_itr = 5000000的情况, 总共计算量一个小时, 结果如下:

Can't keep up!Progress: 99.99%, RSS: 0.21
Optimized Para: [-0.09077744060776945, 0.07166485134075858, 0.32129933494913804, 0.016616009401218938, 0.7692619962190641, 1.0457952702053965, 0.6239775621605967, 0.9694476534866192, -0.048011757100430374, 0.40767881978457904, 0.8671001254228692, 1.0142415688059914, 0.23566596069708334, -0.18036173648964177]
Optimized RSS: 0.20512657082727637

可以看到这个结果已经相当精确了.

b) 数据展示

这里无法避免的使用了plt库.

# 遍历测试集
y_test_pred = [y(_, optimized_para) for _ in test]
test_rss = rss(y_test_pred, [_[-1] for _ in test])

print(f"Test RSS: {test_rss}")

之后绘制三张展示图:

# 训练集预测值与实际值
plt.title(f"y_pred vs y_true in Train")
plt.scatter(range(len(train)), targets, label="y_true", color="#00aaff", alpha=0.5)
plt.scatter(range(len(train)), y_pred_optimized, label="y_pred", color="#aa00ff", alpha=0.5)
plt.legend()
plt.show()

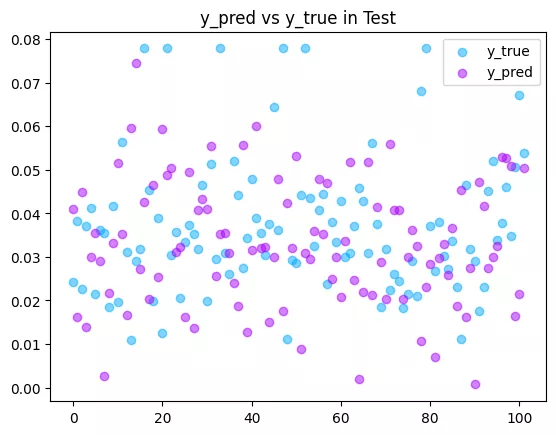
# 测试集预测值与实际值
plt.title(f"y_pred vs y_true in Test")
plt.scatter(range(len(test)), [_[-1] for _ in test], label="y_true", color="#00aaff", alpha=0.5)
plt.scatter(range(len(test)), y_test_pred, label="y_pred", color="#aa00ff", alpha=0.5)
plt.legend()
plt.show()

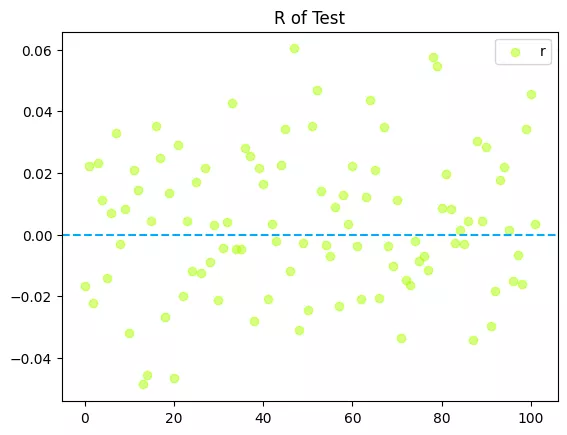
# 测试集残差
plt.title(f"R of Test")
plt.scatter(range(len(test)), [test[_][-1] - y_test_pred[_] for _ in range(len(test))], label="r", color="#aaff00", alpha=0.5)
plt.axhline(y=0, color="#00aaff", linestyle="--")
plt.legend()
plt.show()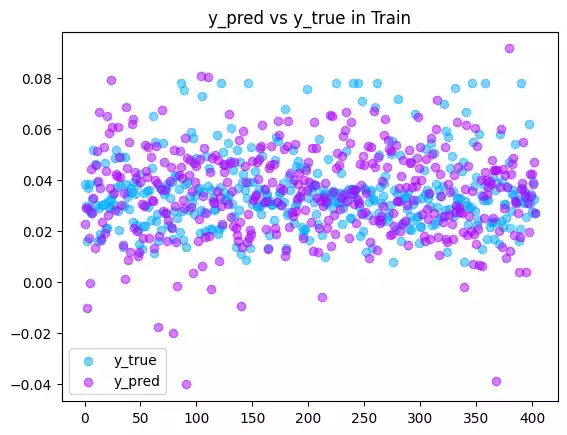

2.5 完整代码

import random
from typing import List
import matplotlib.pyplot as plt

""" 数据导入
"""

data = []
# 按行读取数据
with open("data.txt", 'r') as f:
    for l in f:
        # 按空格划分数据
        line = [float(_) for _ in l.split()]
        data.append(line)

print(f"data: {len(data)}, {len(data[0])}")
size = len(data)

""" 划分集
"""

# 打乱数组, 确保集划分随机
random.shuffle(data)

# 计算大小
train_size = int(size * 0.8)

# 使用切片划分
train = data[:train_size]
test = data[train_size:]

print(f"train: {len(train)}, test: {len(test)}")

""" 数据标准化
"""

# 计算均值
mean = [sum(_)/14 for _ in zip(*train)]

# 更新train和test
for row in range(len(train)):
    train[row] = [train[row][_] / mean[_] for _ in range(14)]

for row in range(len(test)):
    test[row] = [test[row][_] / mean[_] for _ in range(14)]
    
""" 设置参数和函数
"""

# 初始化参数
# lambda_1, lambda_2, ..., lambda_13, delta
para = [1 for _ in range(14)]

# 设置特征值(前13个变量)和目标值(最后一个变量)
features = [sample[:-1] for sample in train]
targets = [sample[-1] for sample in train]

# 设置线性回归函数
# y = lambda_1 x_1 + lambda_2 x_2 + ... + lambda_13 x_13 + delta
def y(x: List[float], para: List[float]) -> float:
    return sum([para[_] * x[_] for _ in range(13)]) + para[13]

# 设置残差平方和函数
# r = y_真 - y_估, rss = r_1^2 + r_2^2 + ...
def rss(y_pred: List[float], y_true: List[float]):
    return sum([(y_pred[_] - y_true[_])**2 for _ in range(len(y_pred))])


# 测试函数(在当前[1, 1, ..., 1]参数下计算残差平方和)
y_pred = [y(feature, para) for feature in features]
print(rss(y_pred, targets))

""" 梯度计算
"""

def get_gradient(features, targets, para):
    # 计算残差
    r = [y(feature, para) - target for feature, target in zip(features, targets)]
    # 初始化梯度
    gradient = [0 for _ in range(14)]

    # 计算lambda偏导
    for i in range(13):
        gradient[i] = sum([r[_] * features[_][i] for _ in range(len(targets))])
    
    # 计算delta偏导
    gradient[13] = sum(r)

    return gradient

""" 梯度下降
"""

def gradient_descent(features, targets, para, learning_rate, tolerance, max_itr):
    # 存储每次的运行结果(内存再见~)
    best_result = [*[0 for _ in range(14)], float("inf")]
    
    # 迭代
    for itr in range(max_itr):
        # 计算梯度
        gradient = get_gradient(features, targets, para)
        
        # 检测是否达到精度
        if all(abs(_) < tolerance for _ in gradient):
            print(f"Done! Itr: {itr}")
            return para
        
        # 参数梯度下降
        para = [para[_] - learning_rate * gradient[_] for _ in range(len(para))]

        y_pred = [y(_, para) for _ in features]
        if rss(y_pred, targets) < best_result[-1]:
            best_result = [*para, rss(y_pred, targets)]
            
        # 打印进度
        if itr % (max_itr // 10000) == 0:
            print(f"Itr: {itr}, Progress: {itr / max_itr * 100:.2f}%, RSS: {best_result[-1]:.2f}", end="\r")

    print(f"Can't keep up!")

    # 获取最优情况
    return best_result[:-1]

""" 应用
"""

# 设置超参数
learning_rate = 0.000001
tolerance = 0.01
max_itr = 5000000

# 开始运行
optimized_para = gradient_descent(features, targets, para, learning_rate, tolerance, max_itr)
print(f"Optimized Para: {optimized_para}")
y_pred_optimized = [y(_, optimized_para) for _ in features]
print("Optimized RSS:", rss(y_pred_optimized, targets))

""" 测试结果
"""

# 遍历测试集
y_test_pred = [y(_, optimized_para) for _ in test]
test_rss = rss(y_test_pred, [_[-1] for _ in test])

print(f"Test RSS: {test_rss}")

# 训练集预测值与实际值
plt.title(f"y_pred vs y_true in Train")
plt.scatter(range(len(train)), targets, label="y_true", color="#00aaff", alpha=0.5)
plt.scatter(range(len(train)), y_pred_optimized, label="y_pred", color="#aa00ff", alpha=0.5)
plt.legend()
plt.show()

# 测试集预测值与实际值
plt.title(f"y_pred vs y_true in Test")
plt.scatter(range(len(test)), [_[-1] for _ in test], label="y_true", color="#00aaff", alpha=0.5)
plt.scatter(range(len(test)), y_test_pred, label="y_pred", color="#aa00ff", alpha=0.5)
plt.legend()
plt.show()

# 测试集残差
plt.title(f"R of Test")
plt.scatter(range(len(test)), [test[_][-1] - y_test_pred[_] for _ in range(len(test))], label="r", color="#aaff00", alpha=0.5)
plt.axhline(y=0, color="#00aaff", linestyle="--")
plt.legend()
plt.show()

数据资料: data.txt